選択した画像 円 性質 109981-円 性質 証明
まず、円に内接する四角形では ∠ A ∠ C = 180 ° が成り立ちます。 対角の和が 180 ° になる理由は、 円周角の定理 から説明できます。 円の中心を点 O 、 ∠ A = θ とおくと 円周角の定理 より中心角は円周角の2倍なので、 青 ∠ B O D ( 青) = 2 θ 次に、一周 円・扇形の公式まとめ 円周: 2πr 2 π r 円の面積: πr2 π r 2 扇形の弧の長さ: 2πr× a 360 2 π r × a 360 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ さっきの「円の接線の性質」、 円の接線は、その接点を通る半径に垂直である をつかえば、 線分pa、qaは円の接線 ってことになるんだね。 これは中2数学でならう内容だから、今はまだわからなくても大丈夫だよー。 まとめ:円の接線の作図は2パターン

円に内接 外接する四角形の性質まとめ 数学の偏差値を上げて合格を目指す
円 性質 証明
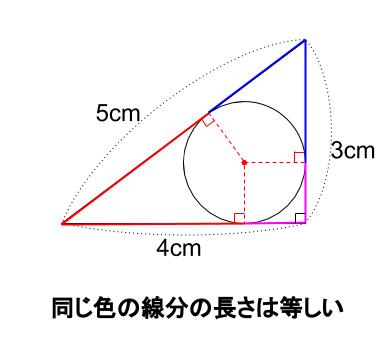
円 性質 証明-問題 下の図のような三角形に内接する円の半径を求めなさい。 解答 超有名問題です。 \(2\) つの解き方を示します。 必ずどちらも理解・暗記しておきましょう。 解法1 円と接線の性質 円の中心と接点を結ぶ線分(半径)は 問題18 次の図は、半径3㎝の円を《ルール》にしたがって、1番目に2個、2番目に3個、3番目に4個、、と並べたものである。 図の太線は、それぞれの図形の周囲を表す。ただし、円周率を$π$とする。 《ルール》 ・それぞれの円の中心が一直線上にある。




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
いよいよ、円の性質っていう単元を勉強していくよ。 今日は、この単元でいちばん大事な、円周角の定理とはなにか??をまとめてみたんだ。計算や証明で使ったりするから、しっかりおさえてあげてね。 = もくじ = 円周角・中心角とは? 高校数学A図形の性質内接円と接線まとめと問題 内接円と接線に関するまとめと問題です。 三角形の各頂点から内接円の接点までの距離や、三角形の面積から内接円の半径を求める解き方について解説しています。 目次 1 内接円と接線 11 内接円の円 $\mathrm O$ の弧 $\mathrm{ST}$ と半直線 $\mathrm{TX}$ が直線 $\mathrm{ST}$ に対して同じ側にあるとき, 次は同値である (i) 直線 $\mathrm{TX}$ は点 $\mathrm T$ で円 $\mathrm O$ に接する (ii) 弧 $\mathrm{ST}$ に対する円周角 $\angle\mathrm{SAT}$ は $\angle\mathrm{STX}$ に等しい
こんにちは。 da Vinch (@mathsouko_vinch)です。 接弦定理接弦定理は「円に内接する三角形とその円に接する接線があり、かつ三角形の"ある"頂点が接点となっている」場合に考えることができます。次のような状態の時ですね円における根幹の性質で,計算でいえば九九くらい大事なポイントです。必ず覚えておきましょう。 関連記事 「円周角の定理の逆」について詳しく知りたい方はこちら 「円と相似の証明問題」について詳しく知りたい方はこちら 3 円の角度を求める問題 中3数学円の性質円周角と中心角:発展編(9~14)のプリント集です。 円に内接する四角形 四角形が円に内接するための条件 接線と弦のつくる角(接弦定理) 2つの円と共通接線 問題・解答解説付きです。 解説動画は下記のリンク先にあります。
円の性質を利用した証明(相似) 円の性質を利用した証明(平行) 円の性質を利用した証明(合同) 円の性質を利用した証明(二等辺三角形) 問題・解答解説付きです。解説動画は下記のリンク先にあります。 テキスト円の性質(15~18)内接円に関しては、作図だけでなく角度を求める問題も出題されるので この性質をちゃんと覚えておく必要があります。 外接円とは 外接円とは、図形の外側にピタッとくっついている円のことですね。垂心の性質《証明》 三角形の垂心がもつ性質の証明をします。 まずは「 四角形adhf,behd,cfheは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。




円の中心と弦 中学3年生 円の性質 数学 Youtube
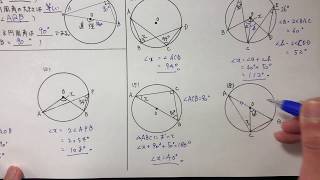



中3数学 円の性質2 円周角と中心角 すべて無料 星組の中学数学講座
三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出 性質1の逆も成立します。つまり, 向かい合う内角の和が 18 0 ∘ 180^{\circ} 18 0 ∘ である四角形は円に内接します。 また,性質1は「外角」を使って表現されることも多いです。さて,円に内接する四角形の性質を考えましたが,実は前項で学んだ定理は,逆も成り立ちます。 逆は,四角形が円に内接するための条件として使えます。 四角形が円に内接するとは,四角形の 4 頂点がすべて同一円周上にあるということです。 この




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4
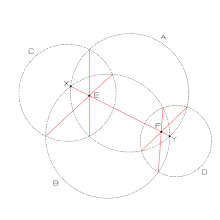



円 数学 Wikipedia
#接弦定理 #円に内接する四角形の性質 #円に外接する四角形の性質ご視聴ありがとうございます。 現役公立中学校教員がはじめました。 ヒント:円の性質を活用してください(円に内接してますよ!!) では、解説に入りたいと思います。 解説 まず、正方形は円に内接しているので、 対角線の長さは、円の直径の長さと等しく cm ですよね続いて図2のように、円の中心Oを1つの頂点とする OABがあるとします。 点OからABに垂線を下ろしその交点をMとしたとき、OMはABを2等分する線になります。 逆を言えば、弦ABの垂直二等分線は、必ず円の中心を通ることになります。 ・数学Aの円で使う定理・性質の一覧




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア
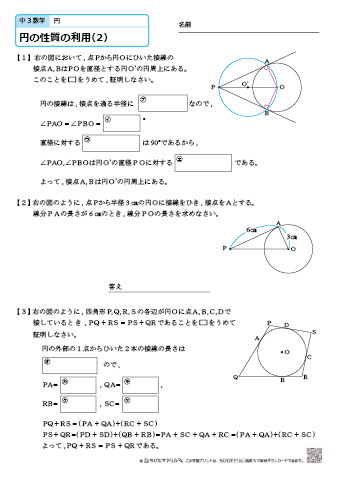



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
円に関する定理や性質 by omusoshiru 公開済み 19年7月13日 更新済み 21年10月22日 1円周角の定理円の性質を見出 し表現すること ができる。 条件に合うように 作図し、円の中に できる角について 考察し、気付いた ことを伝える。 円周角と中心 角に関心をも ち、それらの関 係や性質を見出 そうとする。(観 察・ワークシー ト) 円周角と中心3 性質の例 1つの円では、半径はみんな同じ長さ。 円を半分に折ると、その折れ線は直径と同じ。 直径同士が交わったところはいつも中心と同じ。 直径の長さは半径の2倍。 (2) 定義と性質の指導 円の指導の導入は、およそ次のような展開が用いられてい
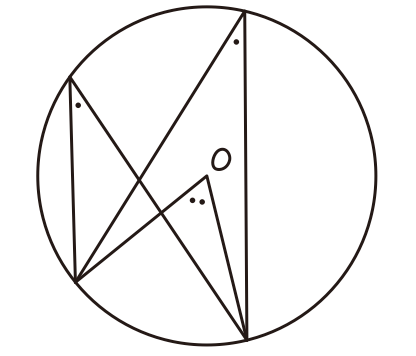



中3数学 円の性質 の重要ポイントをピックアップし 勉強方法を紹介 札幌市 西区 白石区 塾 学習塾 個別指導塾 マナビバ




円に内接 外接する四角形の性質まとめ 数学の偏差値を上げて合格を目指す
ウグイス 円の性質の単元のレポートの問題です。 分からないので教えてくれませんか? A 5 パンフレット問題 F B プ P ある円に2つの三角形が右図のように内接しているとき、 R PB QD RF X の木を見 E =1 PA"OC*RE SPとスク を証明しなさい。 C D 円の性質 内接円の性質 内接円には、\(2\) つの重要な性質があります。 性質① 内心と角の二等分線 多角形の各頂点から内角の二等分線を引くと、必ず \(1\) 点で交わります。その交点が内接円の中心(内心)です。内心と傍心ではまったく違う点に見えますが、 内心と同じような性質を持っています。 内心と傍心のどちらも "角の2等分線の交点" なので似たような性質を持ちます。 その性質のひとつを紹介します。 内心は三角形の内接円の中心の点です。



円に関する定理や性質 わかる数学
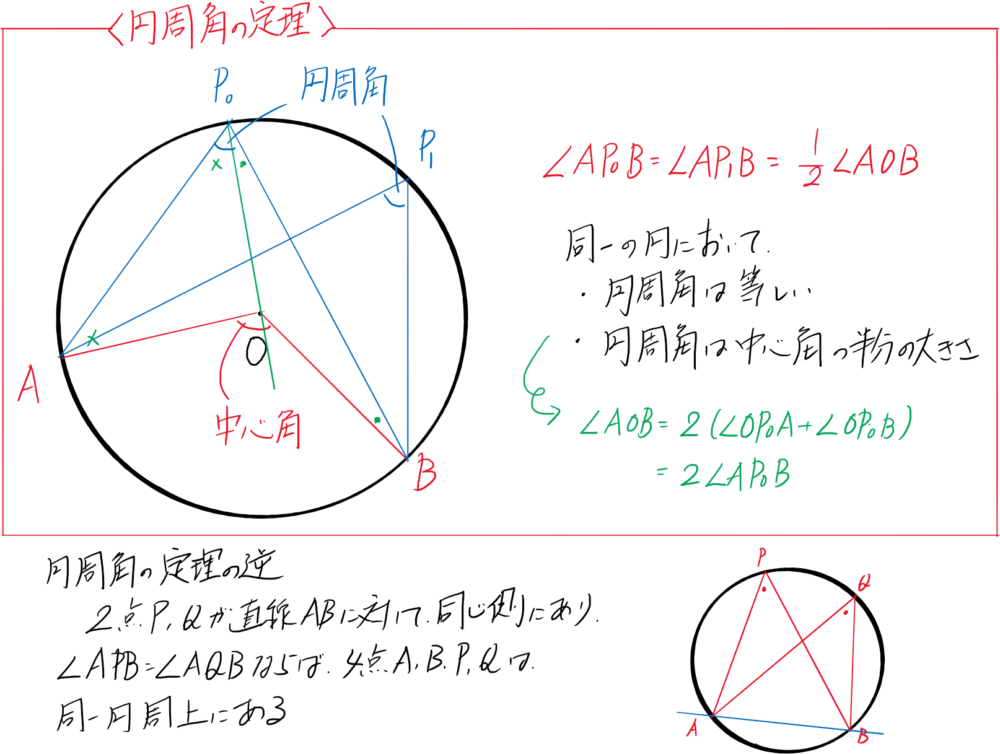



円の性質 円周角の定理 平面幾何 富岡市の総合学習塾 トータルアカデミー
円に内接する四角形の性質 1:円に内接する四角形の対角の和は180° 2:四角形の内角は、その対角の外角に等しい ※ 「円に内接する四角形の対角の和は180°」定理の証明円の基本的な性質 弦、接線、接点という言葉は覚えていますか? その図形的性質は覚えていますか? 覚えていないとまったく問題が解けませんので、必ず暗記しましょう。 弦と二等辺三角形 円 \(o\) と また、交点を中心にして、 三角形の辺に接する ように円を描くと、 三角形の内接円 を描くことができます。 内心を作図してみると、その性質が分かってきます。内角の二等分線を引いたので、 内心は 三角形の辺から等しい距離 にあります 。
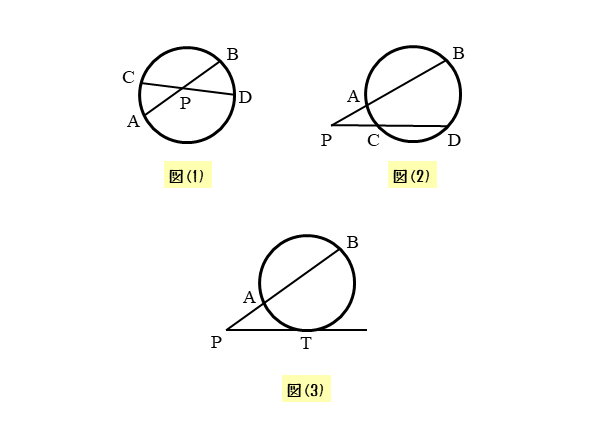



図形の性質 方べきの定理について 日々是鍛錬 ひびこれたんれん



中3数学 円の性質15 円と接線 すべて無料 星組の中学数学講座
数学Ⅰ1数と式 展開公式・因数分解公式α 絶対値の性質・方程式・不等式 平方根の性質・2重根号22次方程式・2次関数 平方完成 2次方程式の解・重解・解の個数 関数の平行移動・対称移動3図形と計量 正弦定理・余弦定理 $90^{ \ 図形と方程式6|2種類の 円の方程式をマスターしよう 前回の記事までで, x y 平面上の点や直線に関する性質について説明しました. 「円」は「中心の位置」と「半径」が分かれば描くことができます. これは,コンパスで円を書くことをイメージすれ円の性質のまとめ ここで4点が同一円周上のあるための条件,直線が円の接線になるための条件に注目して 円の性質をまとめておきます. なお,証明は,最後のトレミーの定理以外,すでに学んだページを参考にして下さい. 命題 四角形abcdで次が成り立つ.
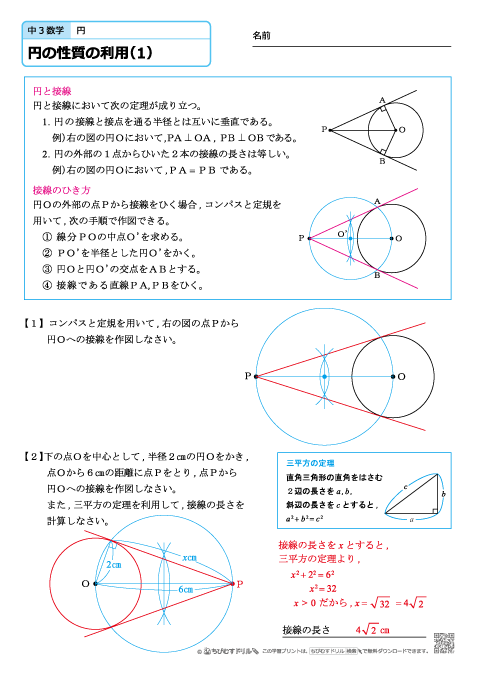



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生



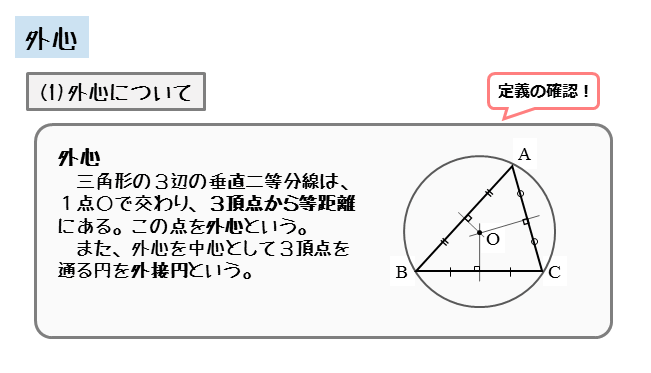
外接円 外心について
MathAquarium練習問題図形の性質 14 14 次の図において,x の値を求めよ。ただし,(3)の直線PT は接点をT とする円の接線である。 (1) (2) (3) Px A 9 D C 5 P B8 6 A D 4 C B x 3 2 P A T B x性質①で述べたように、点qは原点oは通らない点にも注意しましょう 反転の性質③「原点を通る円→原点を通らない直線」 性質の3つ目は 「点pが反転円の中心oを通る円上を動くとき、点qはoを通らない直線上を動く」 です円に内接する四角形の角度 円に内接する四角形の対角の和は 180° である。 → a c = 180°, b d = 180° 円に内接する四角形の外角は,対角 (内角)に等しい。 → a の外角は c の角度と同じ。 証明 ここでは,a c = 180 を説明 (証明)します。 円 周 角 : に 対
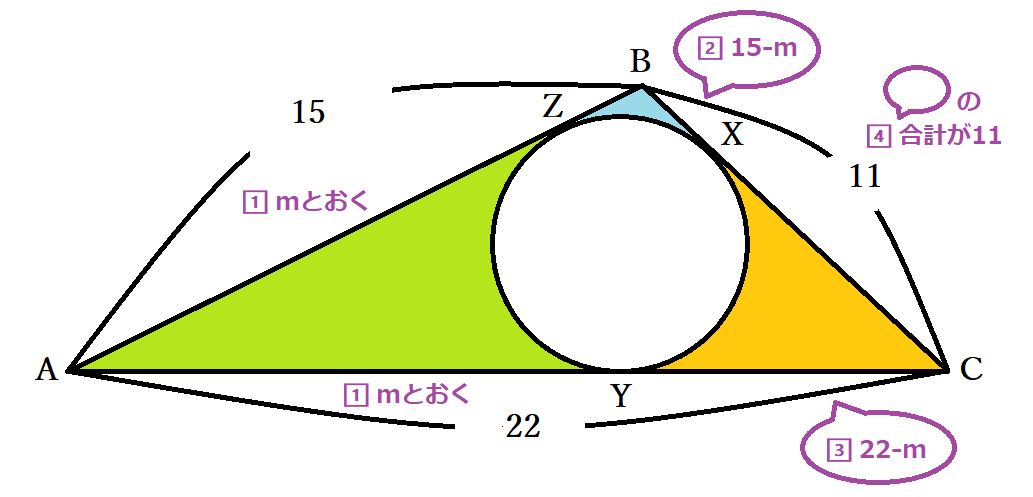



円の接線の性質 公式 円外の点pを通る円oの接線の長さが等しいことの証明 中学数学 Curlpingの学びblog



中3数学 円の性質1 円周角と中心角 証明 すべて無料 星組の中学数学講座
円の性質 弦と弧 円周と2 点で交わる直線を割線という。 このときの交点を 2 点 a, b とするとき、円周によって、割線から切り取られる線分 ab のことを弦といい、弦 ab と呼ぶ。特に円の中心を通る割線を中心線という。中心線は円の対称軸であり、円の面積を 2 等分する。2 2 つの円の位置関係 平面上に 2 2 つの円があるとき,それらの位置関係は以下の 5 5 つのパターンに分類されます. 外部,内部にあるときは共有点は 0 0 個であり,内接,外接のときは共有点はちょうど 1 1 個であり, 2 2 点で交わるときは共有点は 2 2 個
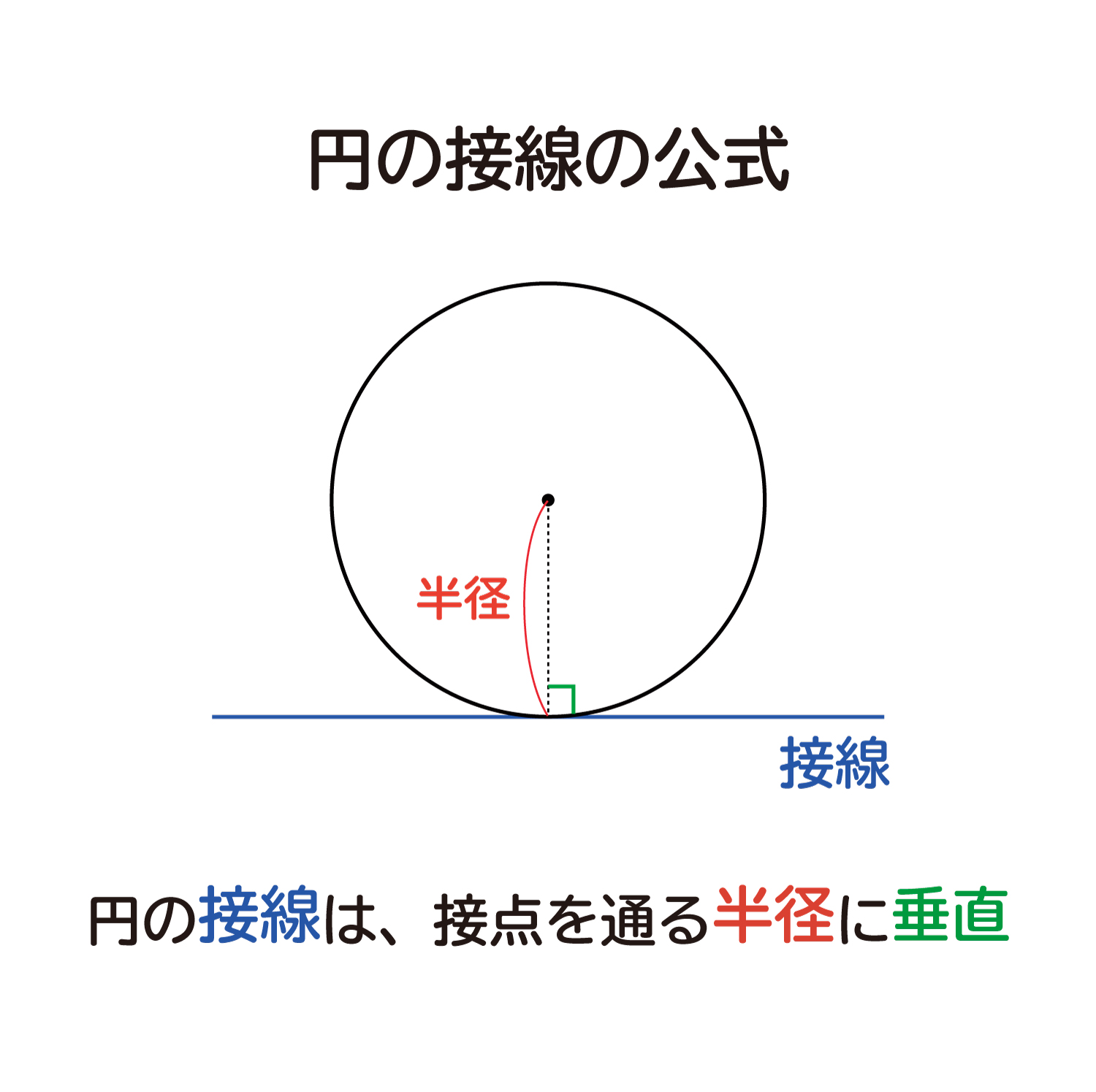



なぜ 円の接線は 接点を通る半径に垂直 になるのか を説明します おかわりドリル




図形の性質 方べきの定理について 日々是鍛錬 ひびこれたんれん




中3 中3 円周角の定理 円の性質の利用 中学生 数学のノート Clearnote
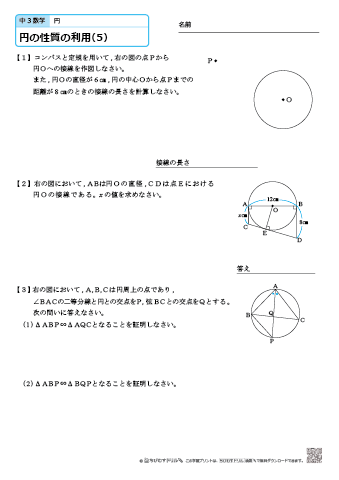



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生
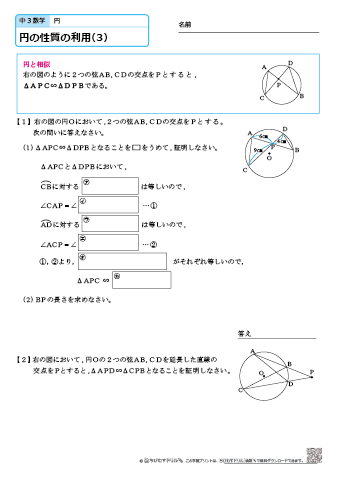



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット
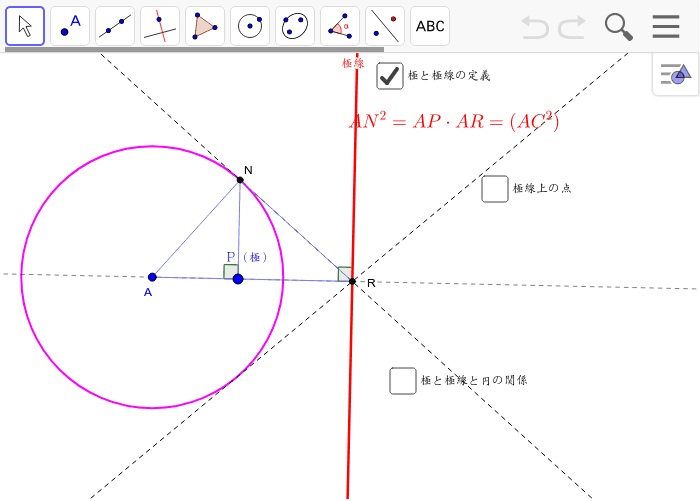



円の極と極線の性質 Geogebra
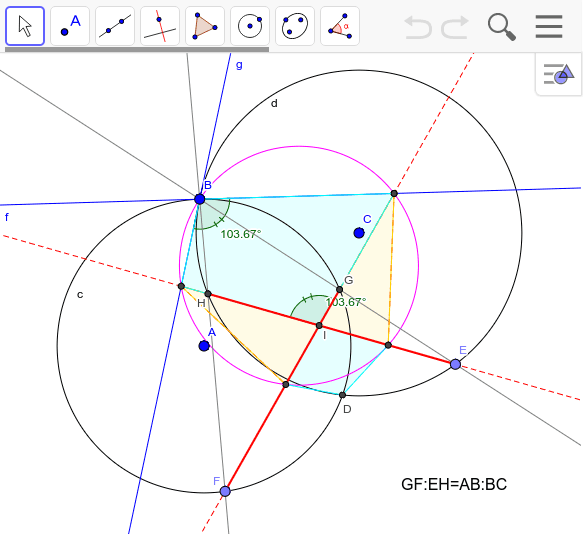



交わる二つの円に関する性質 Geogebra
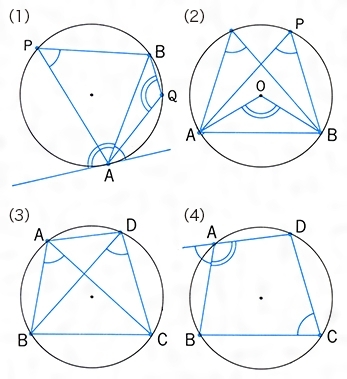



円周角とは コトバンク




円の性質の利用についてです Clearnote



1



P6 円周角の定理 問3 公立高校入試問題 かずお式中学数学ノート 中3 円の性質 三平方の定理 朝日学生新聞社 Youtube
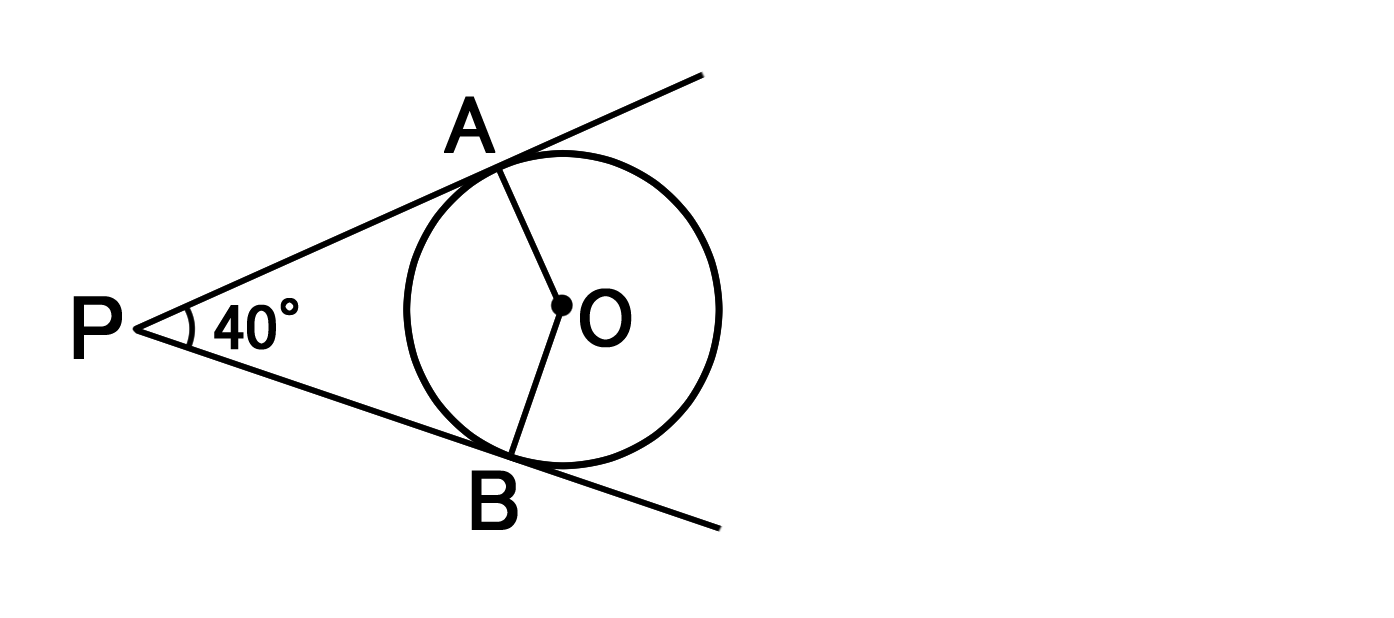



円と接線の性質を利用して図形の角度を求める問題 バカでもわかる 中学数学



1




中3数学 円の性質18 円の性質を利用した証明 すべて無料 星組の中学数学講座
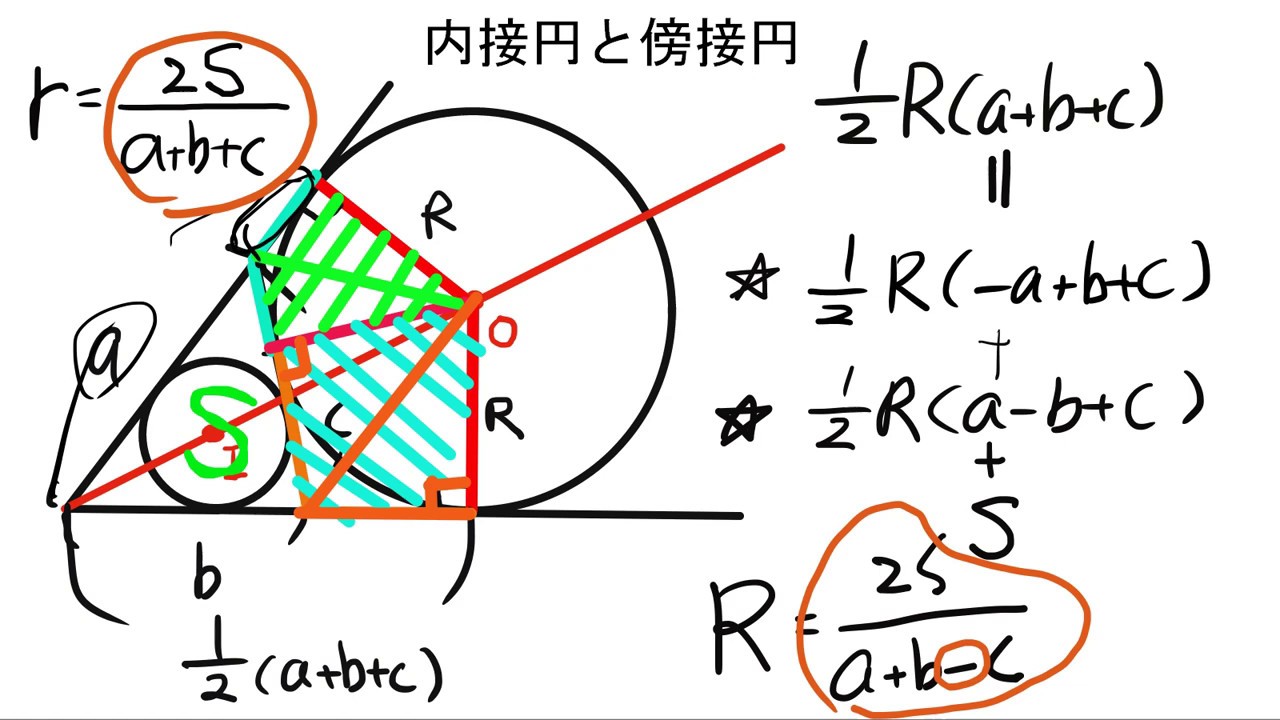



内接円と傍接円の半径公式 Youtube
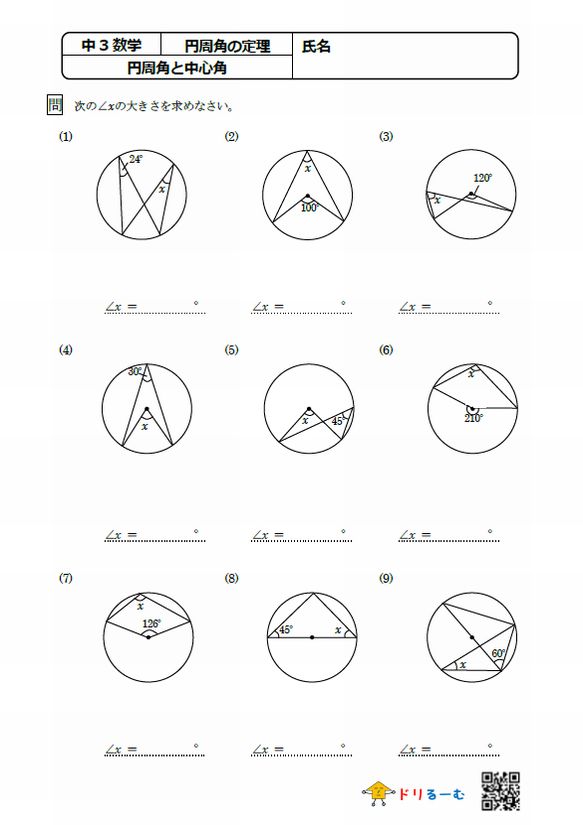



円の性質 ドリるーむ




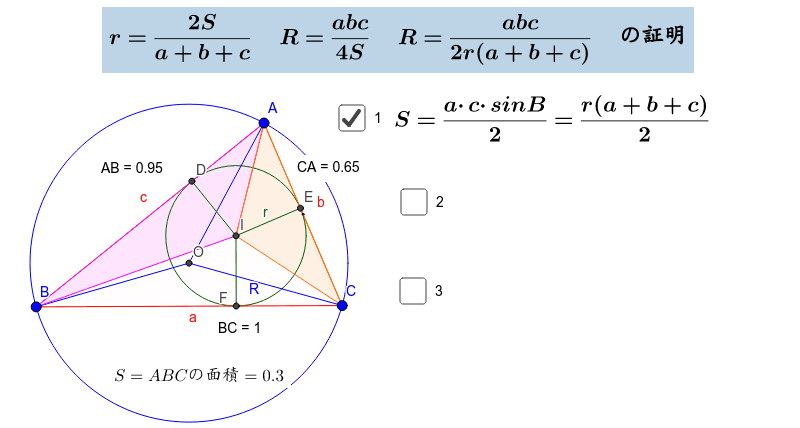
外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ
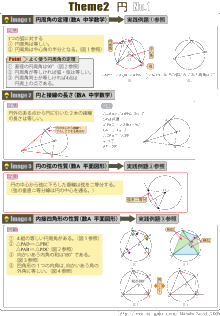



円 に関するチャートを作ってみました 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc




数a 図形の性質 要点まとめ 円編 高校生 数学のノート Clearnote




高校数学a 図形の性質 内接円と接線まとめと問題
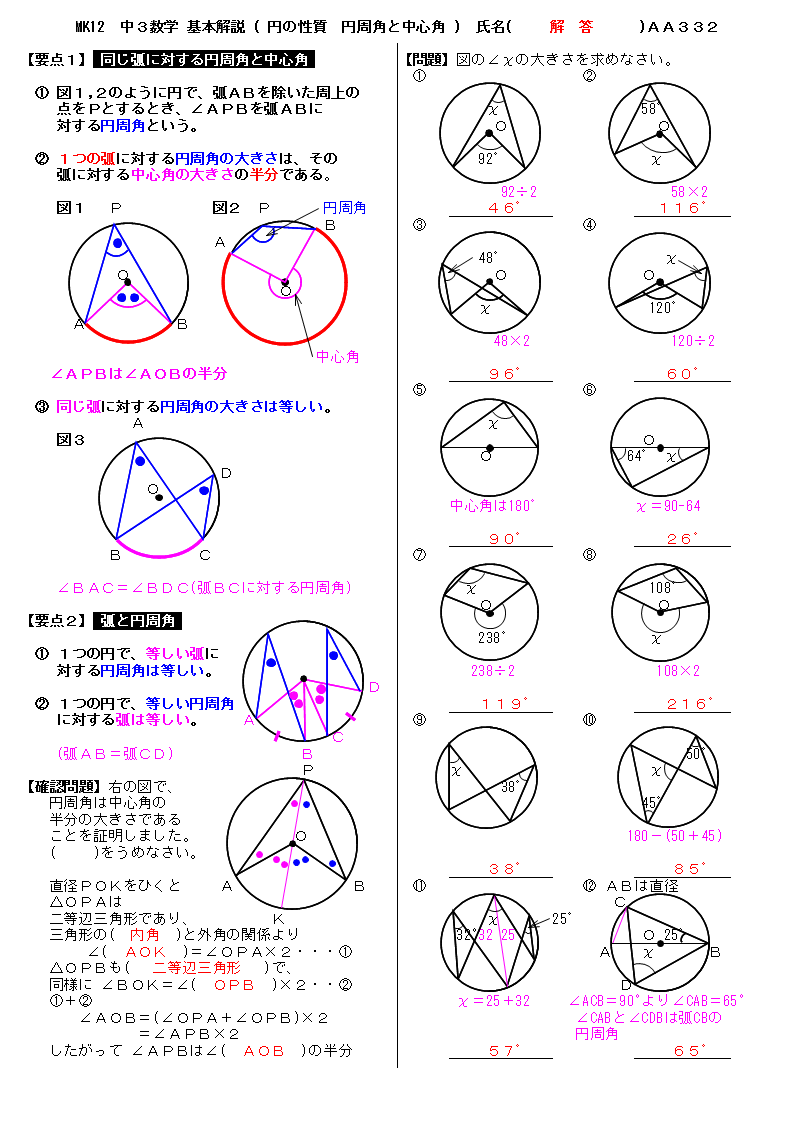



無料 中3数学 基本解説 解答プリント 332 円の性質 円周角と中心角
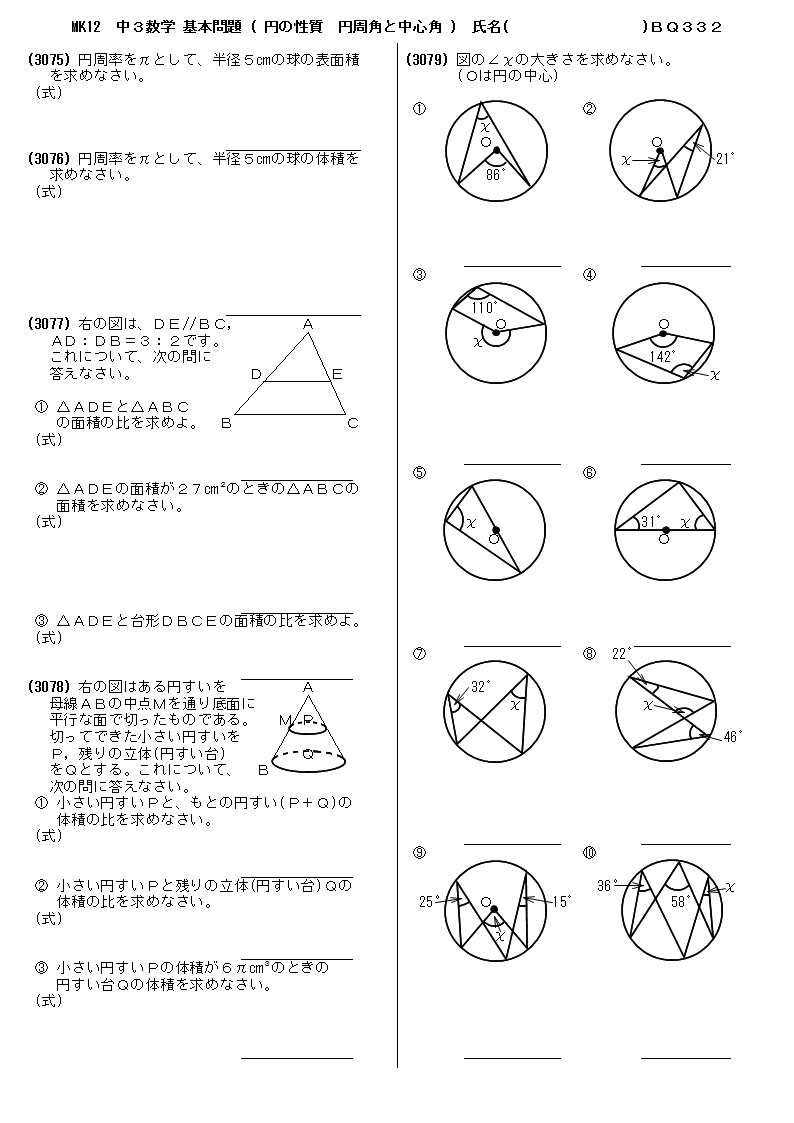



無料 中3数学 基本問題 問題プリント 332 円の性質 円周角と中心角




数学a基礎 図形の性質 演習コース 数学a基礎 演習コース 石井大裕 数学 Kindleストア Amazon




三角形の外接円の 4 つの性質 証明付 理数アラカルト
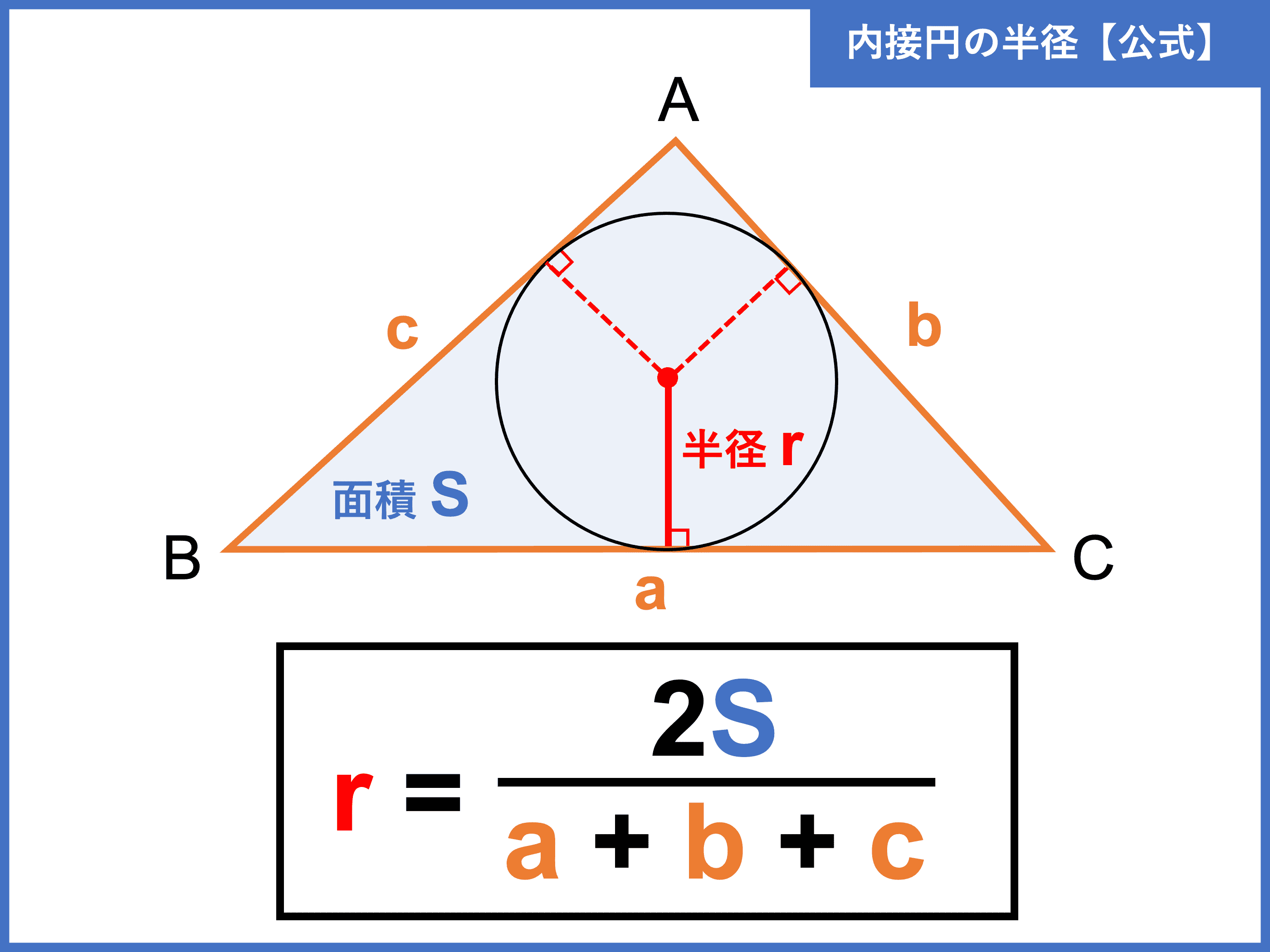



内接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典
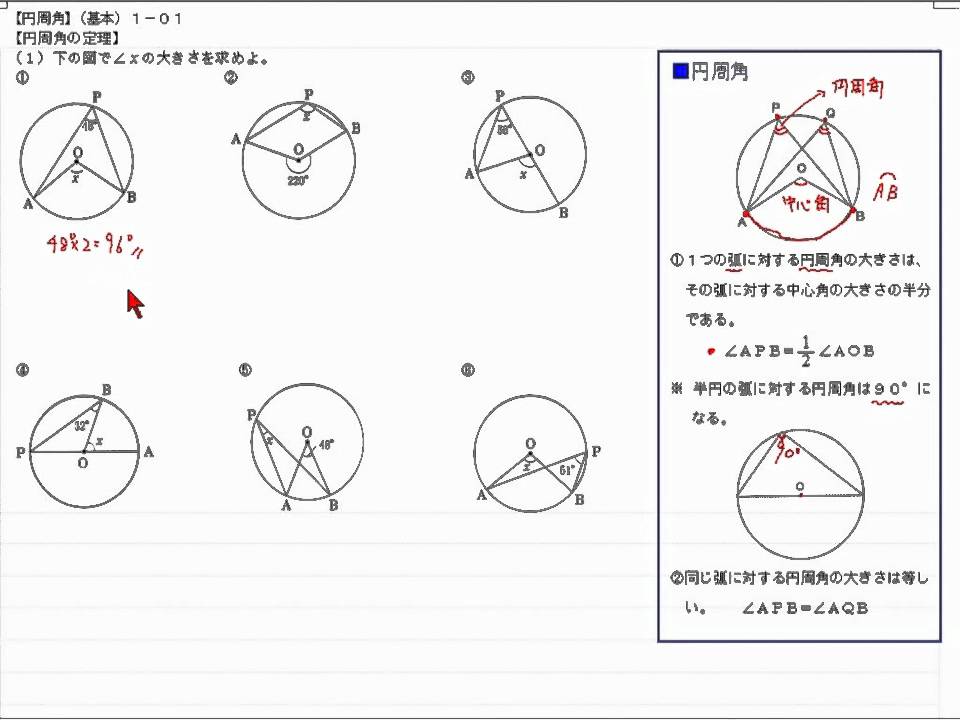



No 295 中3数 円の性質 円周角 基本 1 01 ネット塾の英進塾 Youtube




数学aの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア




数学a 平面図形 円にまつまる問題チャート まとめ集 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru
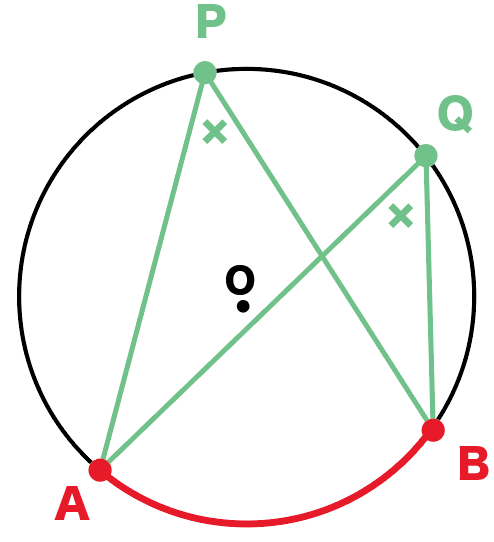



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく
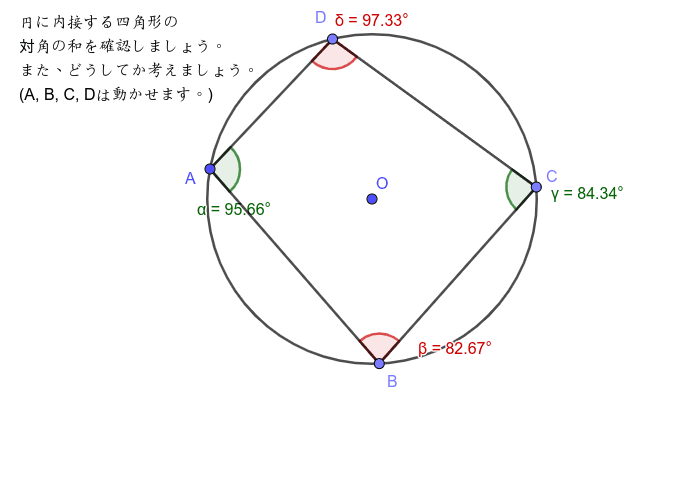



円に内接する四角形の性質 Geogebra



Studydoctor円に内接する四角形の性質 中学3年数学 Studydoctor



中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ



外接円とは 半径の公式や求め方 性質をわかりやすく解説 受験辞典
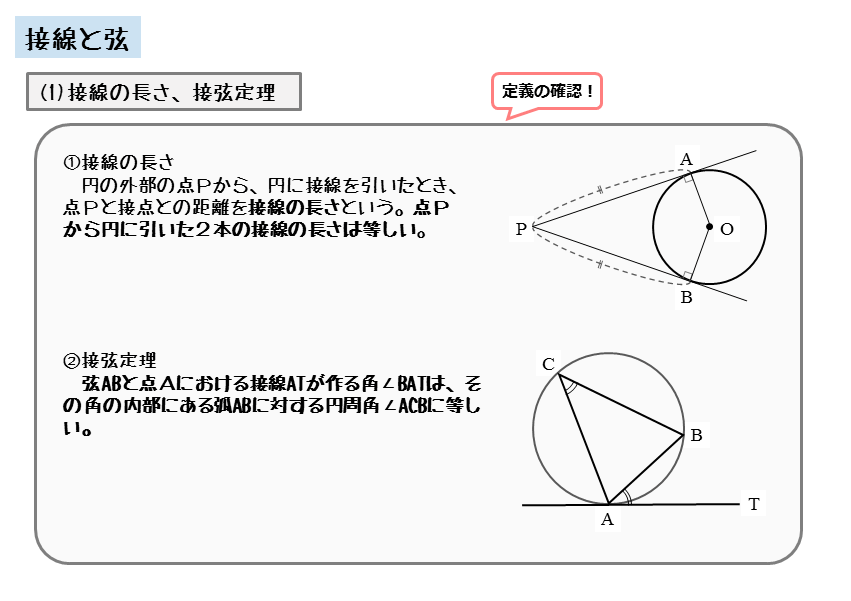



図形の性質 接線と弦について 日々是鍛錬 ひびこれたんれん
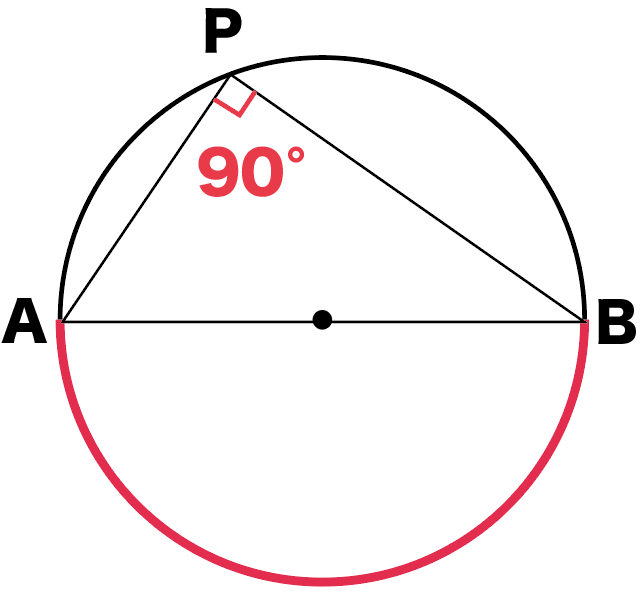



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく
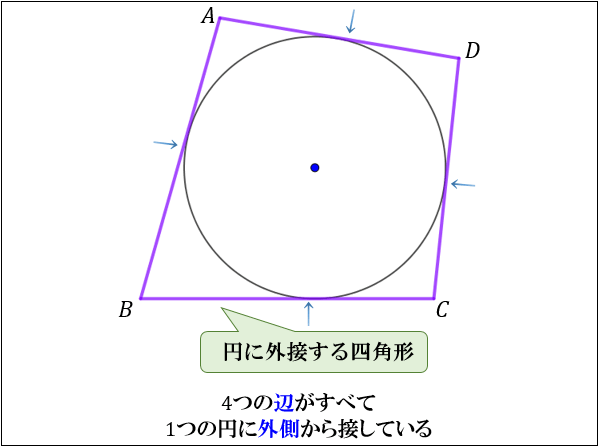



円に外接する四角形の性質まとめ 向かい合った辺の合計が等しくなる理由 アタリマエ
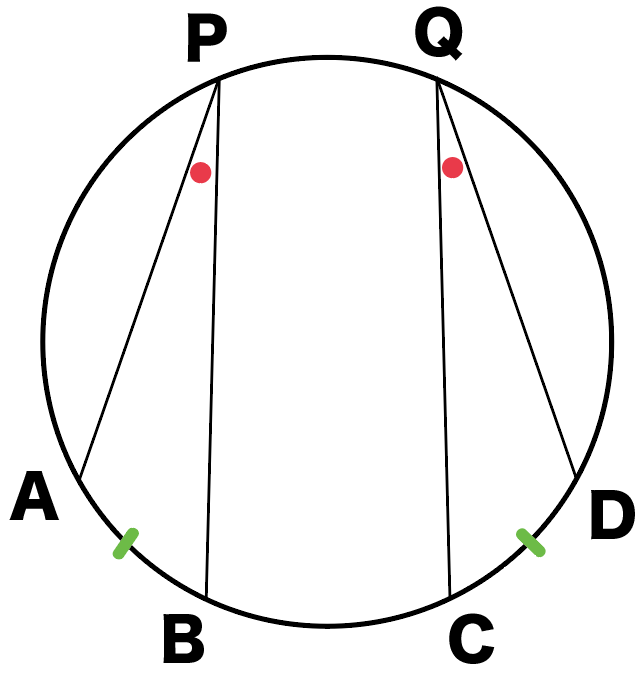



中学数学で役立つ 円周角の3つの性質 Qikeru 学びを楽しくわかりやすく
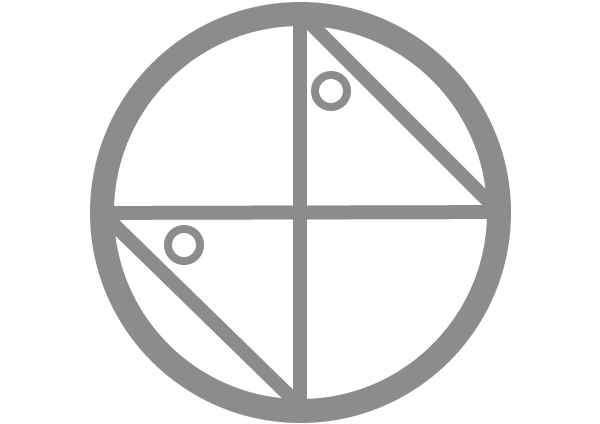



円の性質 円周角 図形 数学 高校受験講座 東京先生




円の性質と円の条件 感じる科学 味わう数学



3



円周角の定理とは 定理の逆や証明をわかりやすく解説 受験辞典
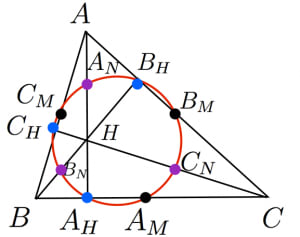



九点円の定理の証明と諸性質 高校数学の美しい物語




円の性質 の勉強法のわからないを5分で解決 映像授業のtry It トライイット



数学a 平面図形 円の性質 方べきの定理
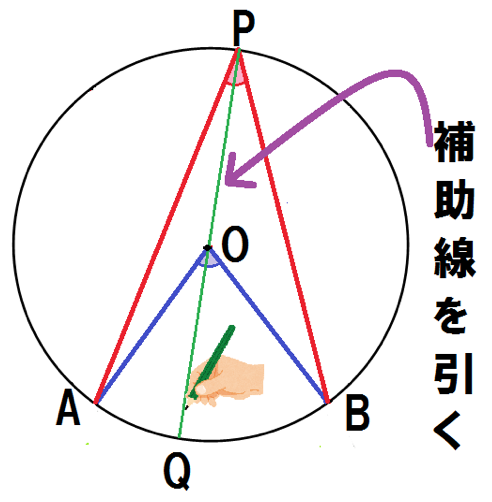



円の性質 Qikeru 学びを楽しくわかりやすく




中学数学 円と接線 Youtube




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット




外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




円の性質 Qikeru 学びを楽しくわかりやすく




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
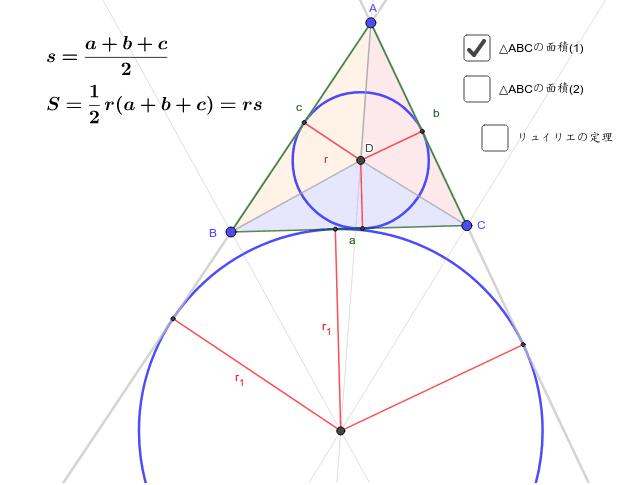



内接円と傍接円の半径 Geogebra
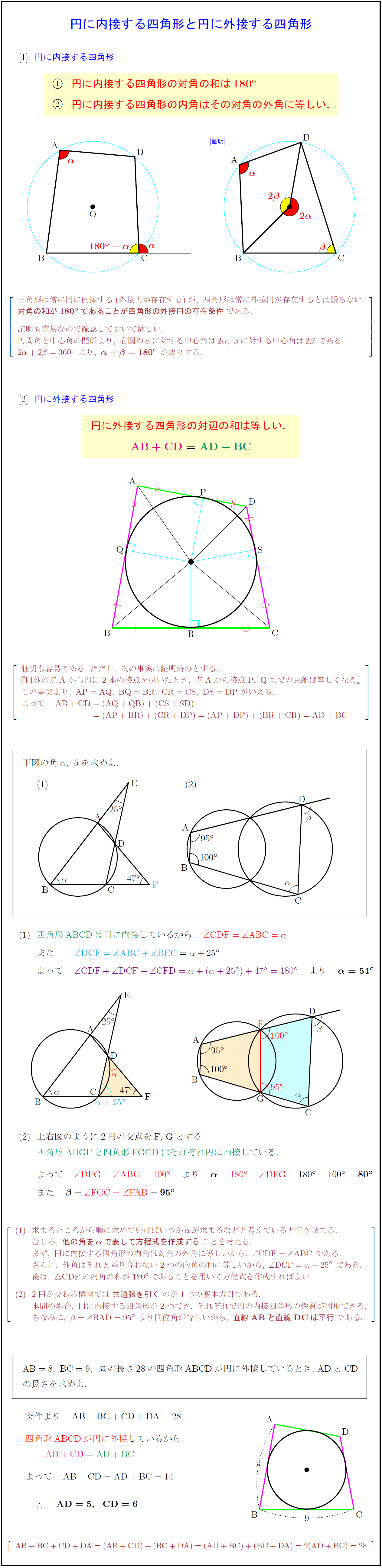



高校数学a 円に内接する四角形と円に外接する四角形の性質の証明 受験の月
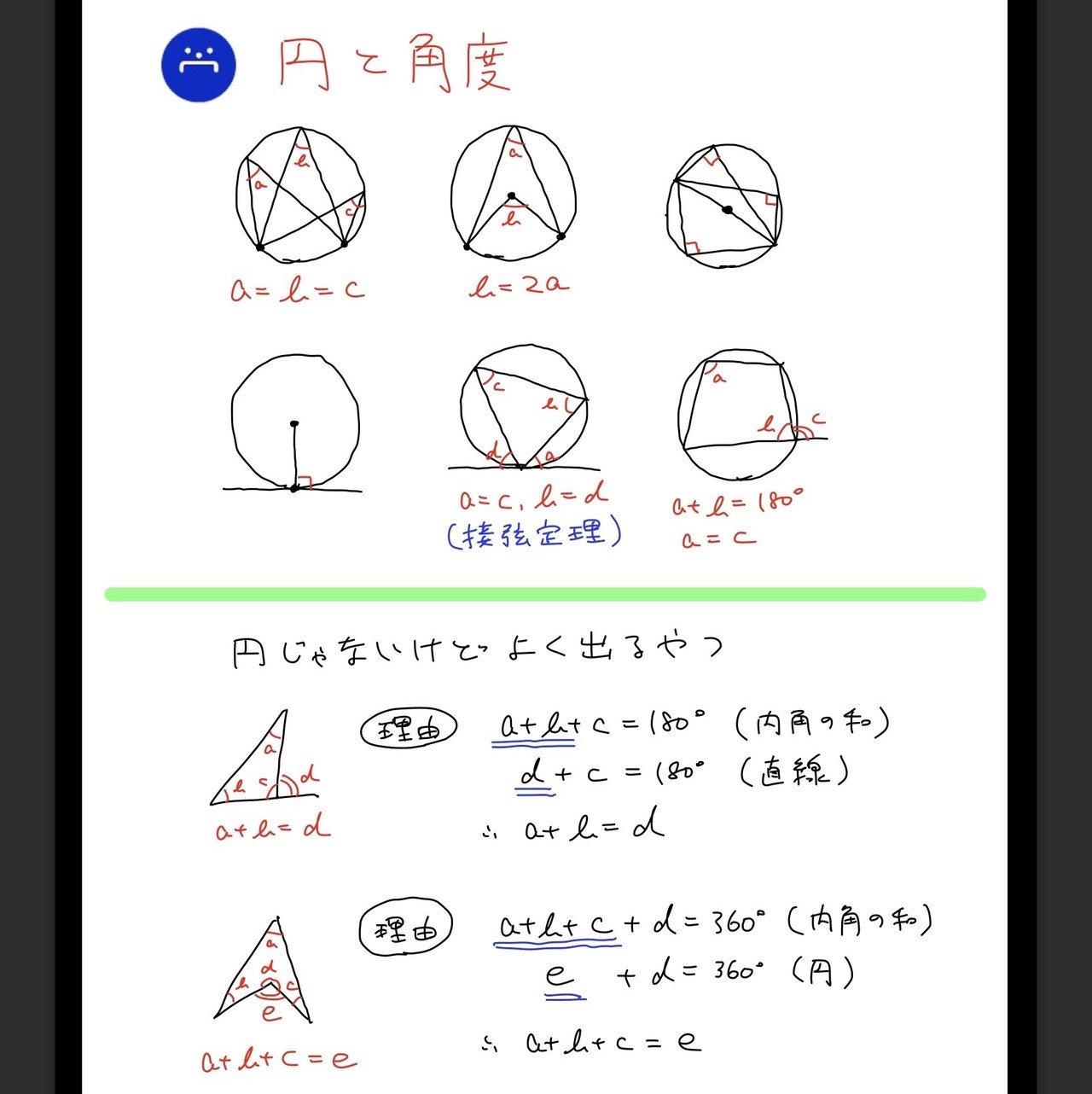



高校数学無料問題集 数a 第2章 図形の性質 円に関する問題 桝 ます Note
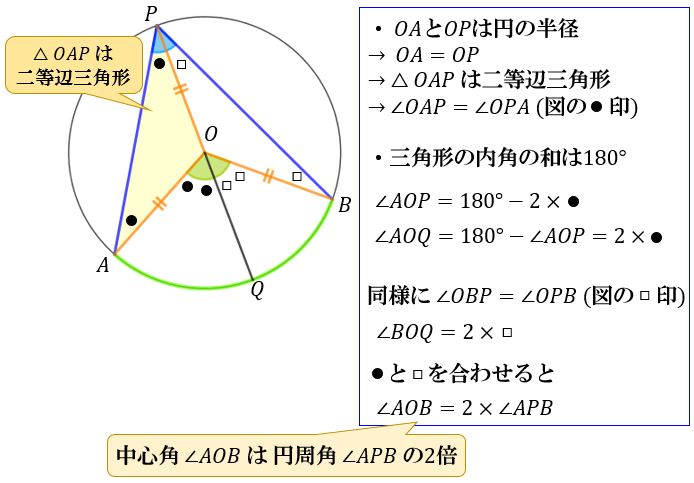



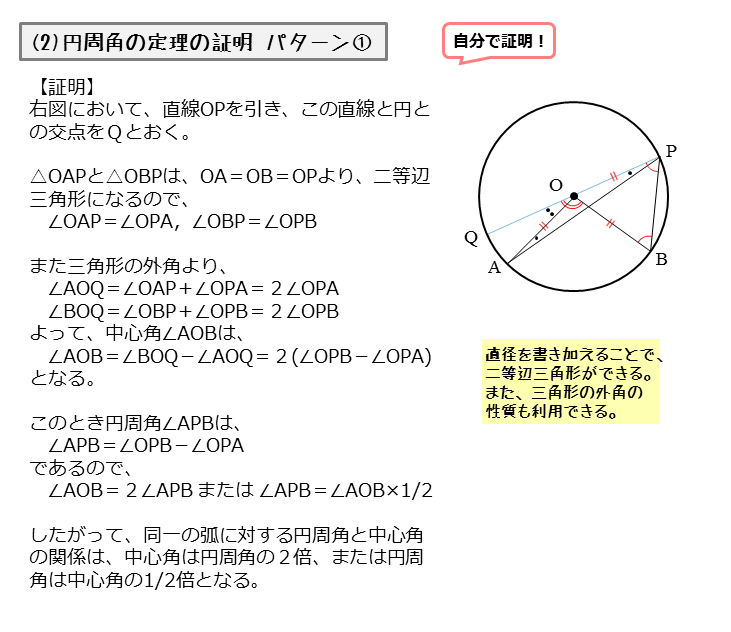
円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット



1
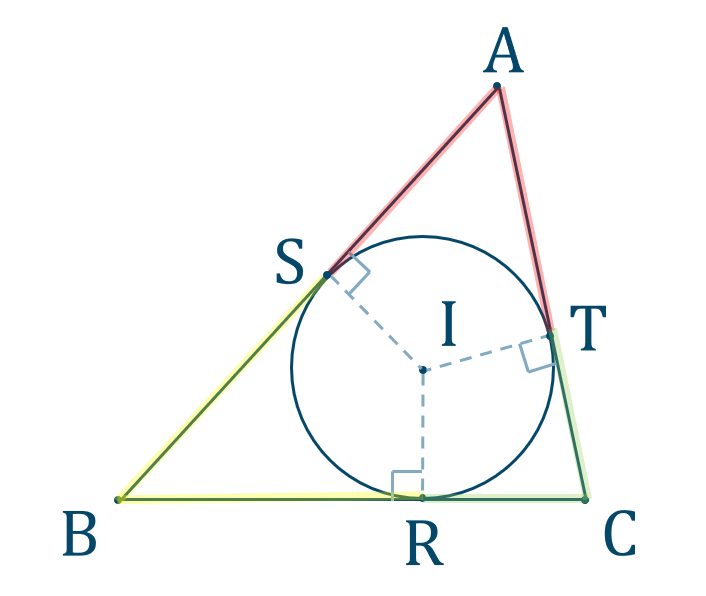



公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学
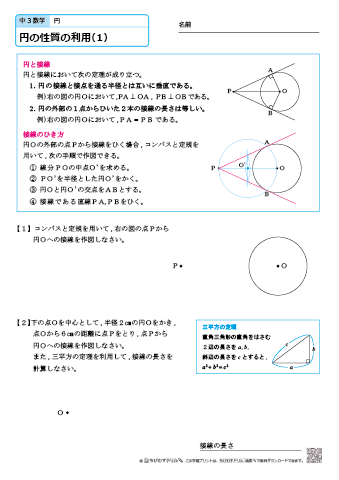



中学3年生 数学 円の性質の利用 練習問題プリント ちびむすドリル 中学生




中3数学 円の性質16 円の性質を利用した証明 Youtube



円 数学 Wikiwand




中3数学 円の性質17 円の性質を利用した証明 すべて無料 星組の中学数学講座



円の性質 Twitter Search Twitter



世界一わかりやすい数学問題集中3 6章 円の性質



三角形の内接円 中学数学の無料オンライン学習サイトchu Su
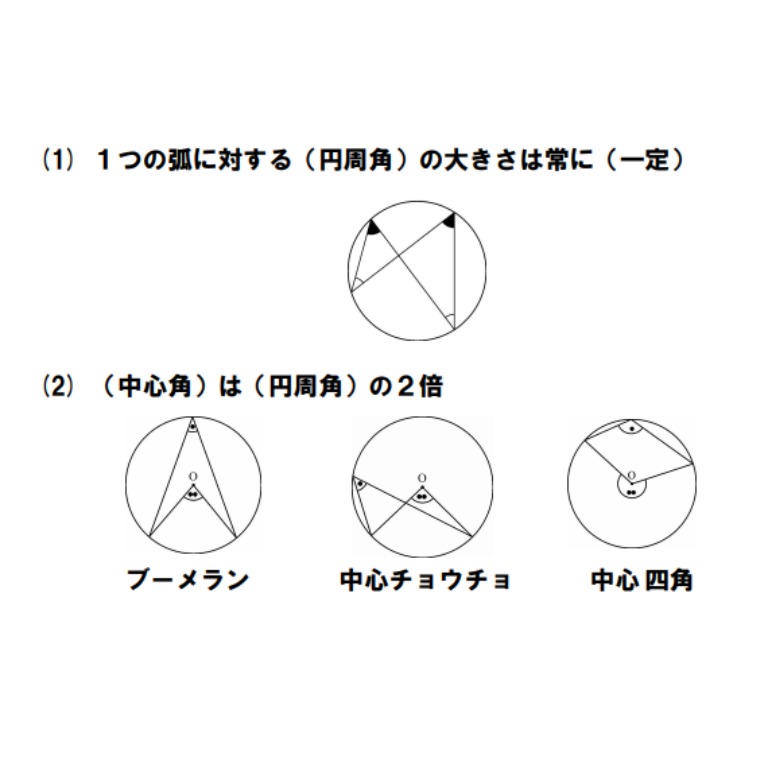



Tossランド 円周角の定理の基本 まとめプリント Dl可




円に内接する四角形の性質 中学数学の無料オンライン学習サイトchu Su




円の性質 の問題のわからないを5分で解決 映像授業のtry It トライイット




6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 2 4
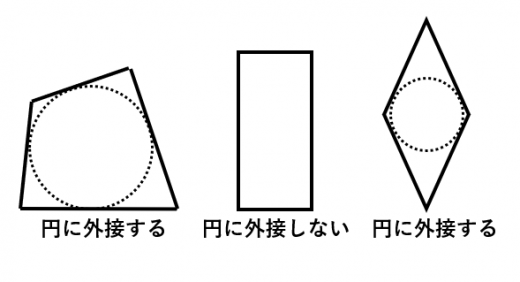



円に外接する四角形の重要な2つの性質 高校数学の美しい物語
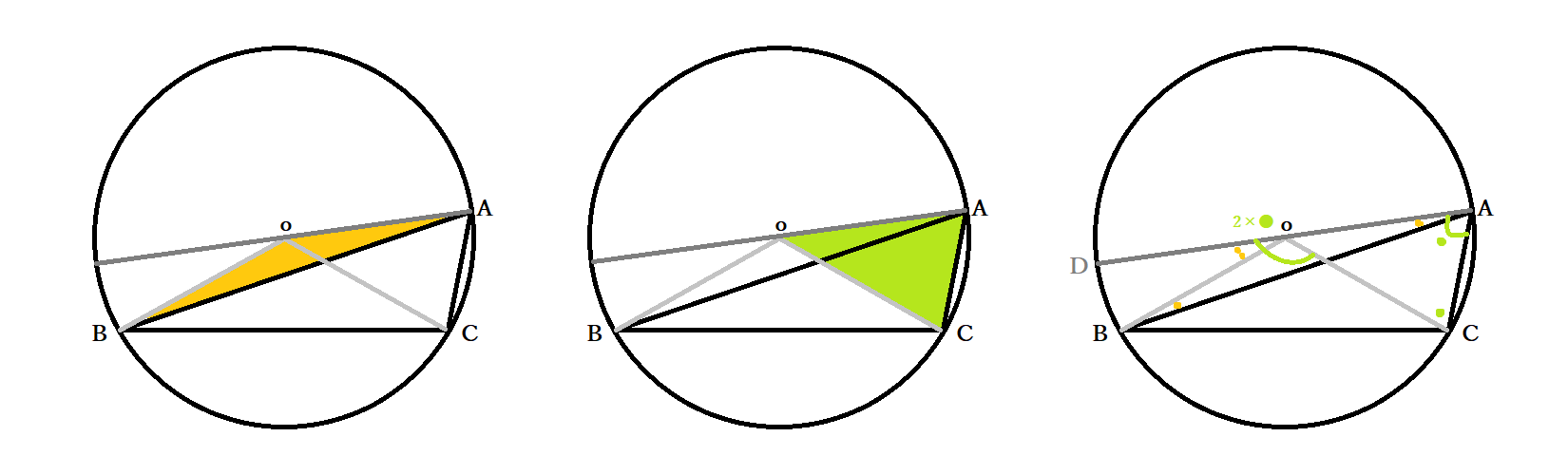



中3数学 円周角の定理とは 円周角と中心角の関係の証明法 円の性質の応用問題 中学 Curlpingの学びblog



2




三角形の外接円の 4 つの性質 証明付 理数アラカルト
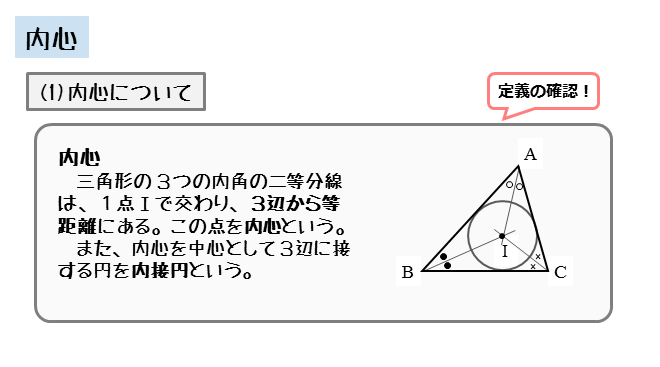



図形の性質 内心について 日々是鍛錬 ひびこれたんれん



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




内接円の半径の求め方 楽に求める時間の節約術とは 高校生向け受験応援メディア 受験のミカタ




中学生 円の性質のノート一覧 Clearnote



外接円の半径 Geogebra
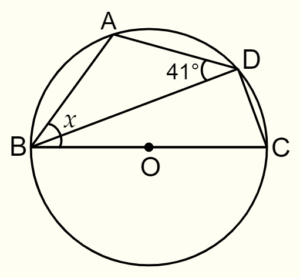



問題 解説 平面図形 円周角の性質を理解するための練習問題 基礎1 数学基礎トレーニングルーム
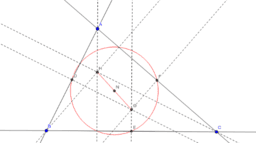



9点円 三角形の不思議な円 Geogebra
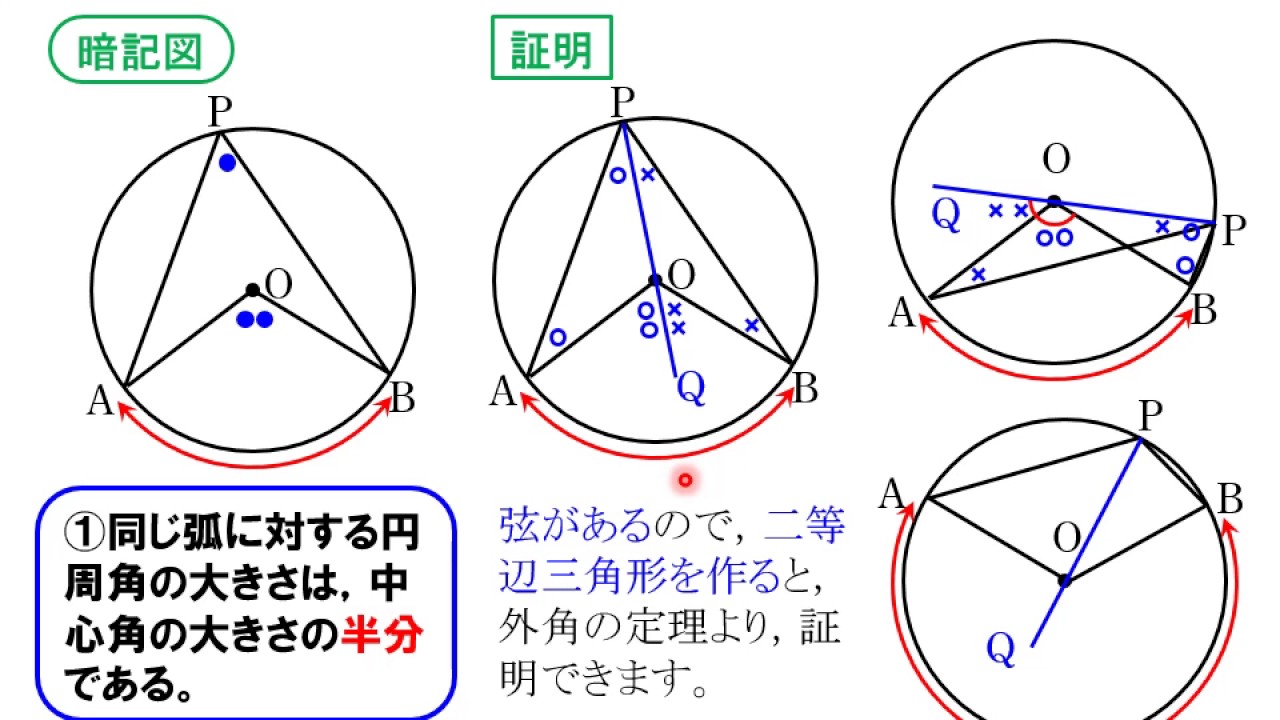



円と角度02 円周角の性質 Youtube



数学a 平面図形 円の性質 円の接線



円 数学 Wikipedia
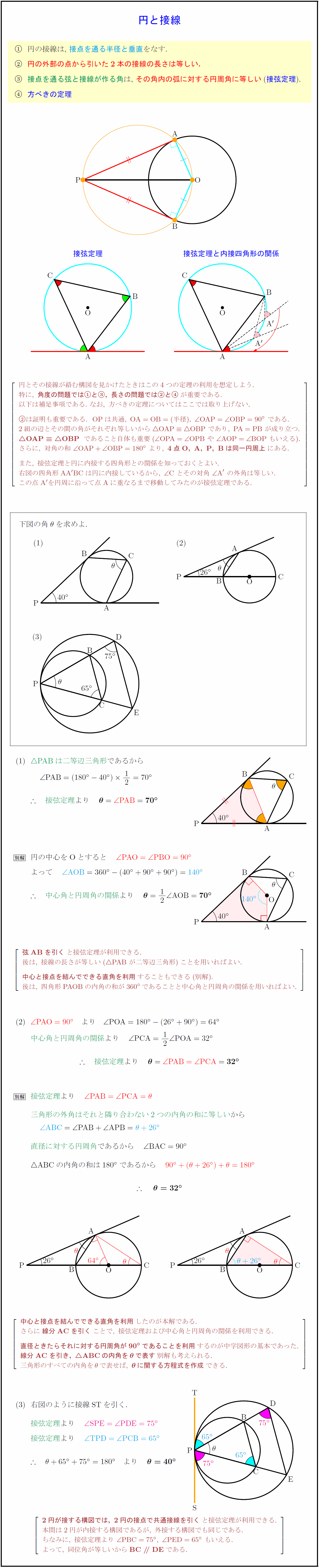



高校数学a 円と接線に関する3定理 垂直 接線の長さ 接弦定理 受験の月
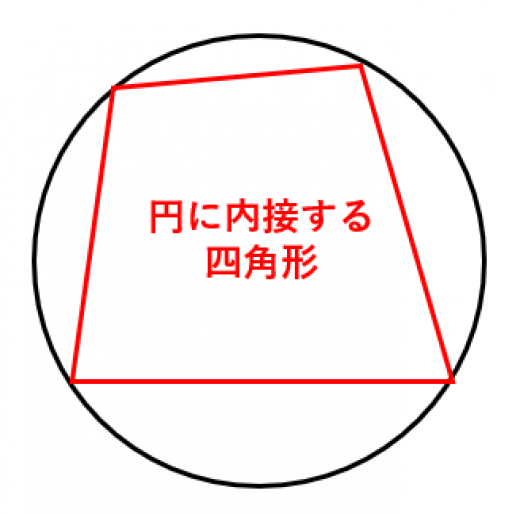



円に内接する四角形の性質とその証明まとめ 高校数学の美しい物語



図形の性質 外心について 日々是鍛錬 ひびこれたんれん




三角形の内接円の半径の求め方 公式 練習問題付き 理系ラボ

No comments: